Lol math

I didn't learn it then, I refuse to learn it now.

My daughter’s teacher sends out a lovely email each week to keep us abreast of third grade happenings. It goes without saying that teachers do unfathomably important work and they should be paid a minimum of a million dollars per day. My undying love and appreciation for teachers has nothing to do with the following screed, which is directed at one thing and one thing alone: MATH.

Here’s a line I found in one of the weekly updates nestled under the heading entitled “Math.”

We applied the distributive “break apart” property to arrays.

I have many questions and concerns.

1. When the word “apply” is used in a mathematical context, I experience PTSD symptoms. Math was chill when it was addition and subtraction. It was fine when it was multiplication. Long division was a bit dicey but for the most part, reasonable. Fractions and decimals were fucked. Algebra was magical thinking. Geometry was supposed to be about shapes but instead ended up being about nothing.

2. The word “distributive” is definitely a math word I have spent most of my adult life trying to forget. I never fully learned what it meant then and I sure as hell won’t subject myself to the pain of relearning what is now.

3. “Break apart” seems ok, right? I know how to “break apart” a piece of bread. I know how to “break apart” from a group of people talking about something I’m not interested in (math, for example). But because “break apart” is part of a math sentence, you know it’s violent chaos disguised as simple language.

4. Re: “property,” refer to concern #2.

5. ARRAYS HAHAHAHAHAHA.

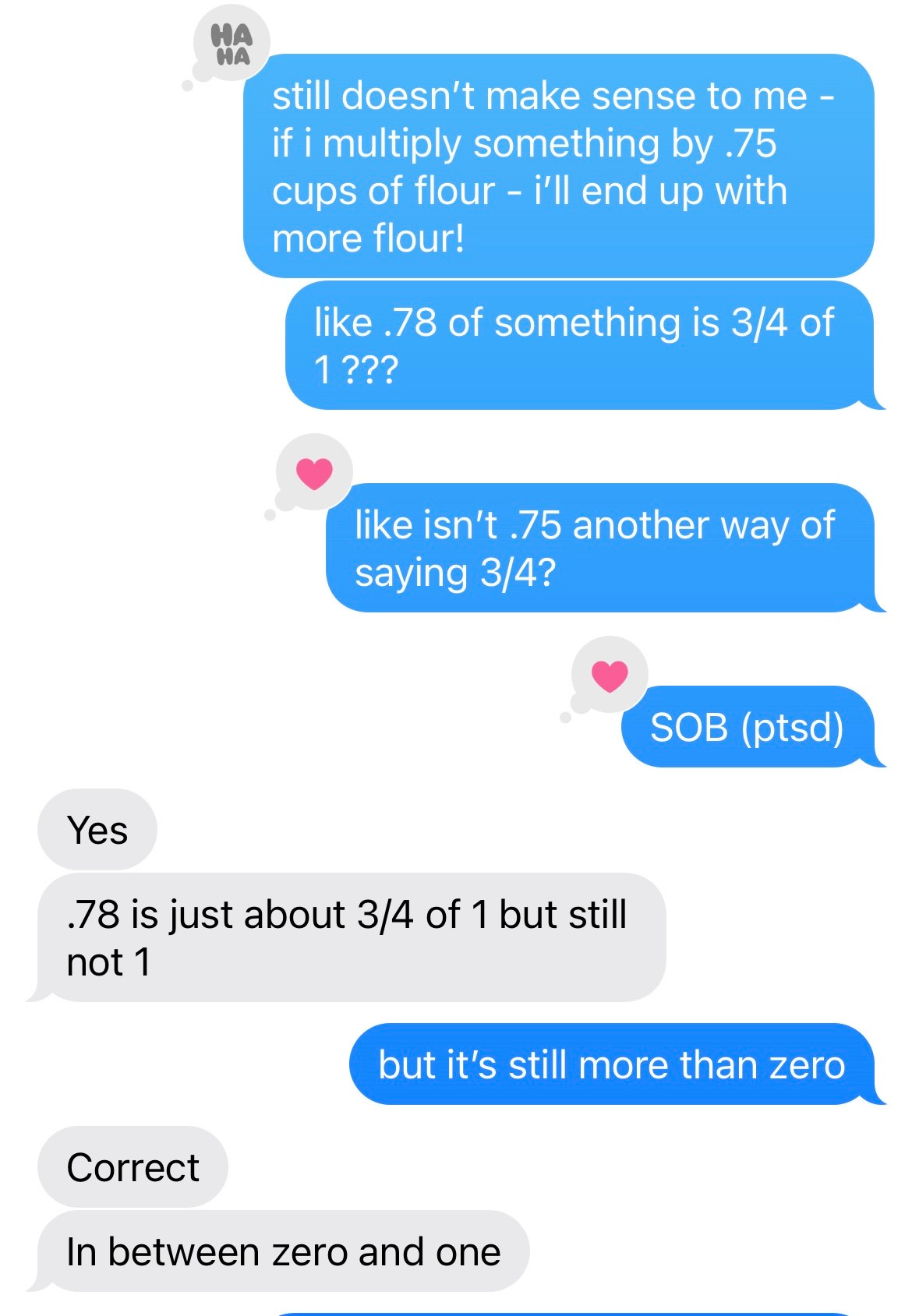
See also this conversation between me and my cousin in which I try to understand why I’m multiplying a number by .78 to convert Canadian dollars to American dollars (or was it vice versa? Who knows! Definitely not me!) We had gone to Canada with friends and were trying to figure out Venmo hell. If you multiply something by something, the resulting number SHOULD BE BIGGER according to this Merriam Webster definition, and yet, MATH defies logic and declares that sometimes a number becomes SMALLER when multiplied.

“GREATER IN NUMBER” NOT “SMALLER IN NUMBER.” SIMPLE FACTS.

Please understand, this thread went on and on and spanned several days, and I’m zero steps closer to understanding why the fuck a number can possibly become smaller when multiplied by another number.

See also, this episode of Poog which taught me more about math than a decade of schooling.

Conclusion: My math career was over as soon as it was legal* to opt out and no one ever told me I’d have to learn math as an adult so I could help my kids learn math so I politely and respectfully decline. Godspeed to my sweet child and her adventures with “applying the distributive ‘break apart’ property to arrays.”

I wish her well.

* In my case, this mean Algebra II was the end of the road in high school, and since I went to an artsy undergrad college, getting over a 500 on the math portion of your SATs precluded you from needing to take any math courses in college. I got a 510. Long live artsy liberal arts colleges.